Fibonacci in Ruby Hashes

Let's talk Hashes

A Hash is a performant key-value pair store. Performant is important here, as it means that no matter how large the Hash gets, it's still just as quick to find a value.

There are a couple of ways of defining a Hash in Ruby:

• Define the Hash with its key value pairs.
• Instantiate an empty Hash. You can pass in a default value to the Hash when you instantiate it. We will come back to that.

menu = { pizza: 7.99 }
# => {:pizza=>7.99}

menu = Hash.new()
# => {}

There are a few ways to get data from the Hash. You can use the fetch method. This returns a value for the given key. If the key isn't found it will raise an error. You can also access the data by using the key; it will return a value if it exists, or will return a default value if it does not. The default value is nil.

menu.fetch(:pasta)
# KeyError (key not found: :pasta)

menu[:pasta]
# => nil

You can set a default value in two ways: either by using the .default method or by passing in a value when it's initialised.

# Setting the default value using the .default method
menu.default
# => nil
menu.default = 4.99
# => 4.99
menu[:salad]
# => 4.99

# Setting the default value on initialisation
menu= Hash.new(5)
# => {}
menu[:salad]
# => 5

You can also set the default to be a proc. For example, you could create a proc so that, if you look for a key and it doesn't exist, the key is created with a default value.

menu = Hash.new { |menu,item| menu[item] = 4.99 }
# => {}
menu[:ice_cream]
# => 4.99
menu
# => {:ice_cream=>4.99}

Let’s talk Fibonacci

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765

The Fibonacci sequence is a series of numbers, where the next number in the series is calculated by adding up the two numbers before it.

Mathematically, the Fibonacci formula is written like this:

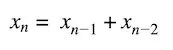
A common starter project for people learning to code is to try and write a program that calculates the Fibonacci sequence.

One possible way of calculating the Fibonacci sequence is to use code similar to that shown in Example 1.

Example 1: Using a function

def fib(n)
  case n
  when 0, 1
    n
  else
    fib(n-1) + fib(n-2)
  end
end

This code works, and is very readable. It essentially describes exactly what it's doing and looks very similar to the mathematical formula. But it has one key flaw. At larger numbers, the computation takes a long time. For each number in the sequence, the function needs to calculate the value -1 and the value -2 and continue to drill down until it reaches 1 or 0. This results in duplication of some of the work that it's doing.

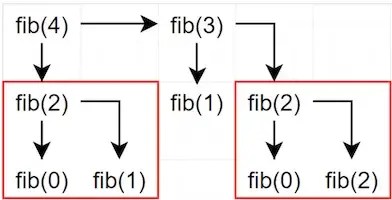
Example 2: Using a Hash

Now let's look at how we can calculate the Fibonacci sequence by using a Hash.

hash = Hash.new { |h,k|
  h[k] = h[k-2] + h[k-1]
}
hash[0] = 0
hash[1] = 1

This code reads in a very similar way to the function example, but the difference is that it comes with caching. This is a form of memoisation. The Hash will look for the specified number; if it doesn't exist, the number will be calculated by using the two numbers that come before it. If those numbers also don’t exist, the Hash will keep running down the chain until it reaches the 0 and the 1.

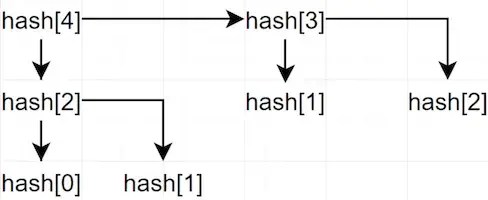
The code in Example 2 doesn't need to calculate values in multiple branches, as it does in Example 1, because the data is already cached at the time the value was first calculated. The second time around, it just needs to read that data.

Conclusion

To test out the differences in performance between these two calculations, I ran each block of code on my machine.

• The code in Example 1 (using a function), calculated the first 35 Fibonacci numbers in a second. The calculation required 29,860,703 calls to the function.

• The Hash version in Example 2 calculated approximately 100,000 Fibonacci numbers in a second. The calculation required 69 calls to calculate 100,000 Fibonacci numbers.

I hope this helps to demonstrate the power of caching in code and sparks some thoughts of new and interesting ways that you can use Hashes.

Inspired by The Humble Hash talk, by Ariel Caplan at RubyConf 2020.